
Surf grass on the rocky reef -- appearing blurred in this time exposure -- is tossed back and forth by powerful ocean waves passing by above. San Clemente Island.
Species: Surfgrass, Phyllospadix
Location: San Clemente Island, California
Image ID: 10237
Species: Surfgrass, Phyllospadix
Location: San Clemente Island, California
Image ID: 10237
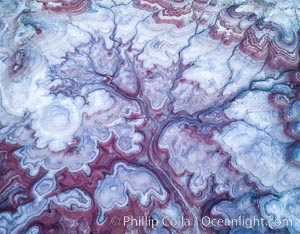
Pre-Dawn over the Tree of Eons, Utah. The Tree of Eons is a spectacular geologic sight near the San Rafael Swell. Erosion has cut a "tree" through red, blue, purple and white layers of the Chinle formation. The Tree of Eons is a superb example of dendritic erosion and to really appreciate the complex fractal-like details it must be observed from above. Photographed here in the soft, predawn light, it takes on magenta, red and purple hues just before the sun reaches it. Aerial panoramic photograph.
Location: Utah
Image ID: 38027
Location: Utah
Image ID: 38027

La Jolla Cove and Point La Jolla at Dawn, waves blur into abstract white, pre-sunrise soft light.
Location: La Jolla, California
Image ID: 38917
Location: La Jolla, California
Image ID: 38917

Scripps Pier, predawn abstract study of pier pilings and moving water.
Location: Scripps Institution of Oceanography, La Jolla, California
Image ID: 37554
Location: Scripps Institution of Oceanography, La Jolla, California
Image ID: 37554

Erosion patterns in the Utah Badlands, aerial abstract photo.
Location: Hanksville, Utah
Image ID: 37948
Location: Hanksville, Utah
Image ID: 37948

Snow geese fly in huge numbers at sunrise. Thousands of wintering snow geese take to the sky in predawn light in Bosque del Apache's famous "blast off". The flock can be as large as 20,000 geese or more.
Species: Snow goose, Chen caerulescens
Location: Bosque del Apache National Wildlife Refuge, Socorro, New Mexico
Image ID: 38742
Species: Snow goose, Chen caerulescens
Location: Bosque del Apache National Wildlife Refuge, Socorro, New Mexico
Image ID: 38742

Ghostly California brown pelican glides over breaking surf, abstract with motion blur and pastel pre-dawn colors.
Species: Brown Pelican, Pelecanus occidentalis, Pelecanus occidentalis californicus
Location: La Jolla, California
Image ID: 37676
Species: Brown Pelican, Pelecanus occidentalis, Pelecanus occidentalis californicus
Location: La Jolla, California
Image ID: 37676

Snow geese fly in huge numbers at sunrise. Thousands of wintering snow geese take to the sky in predawn light in Bosque del Apache's famous "blast off". The flock can be as large as 20,000 geese or more.
Species: Snow goose, Chen caerulescens
Location: Bosque del Apache National Wildlife Refuge, Socorro, New Mexico
Image ID: 38715
Species: Snow goose, Chen caerulescens
Location: Bosque del Apache National Wildlife Refuge, Socorro, New Mexico
Image ID: 38715

Snow geese fly in huge numbers at sunrise. Thousands of wintering snow geese take to the sky in predawn light in Bosque del Apache's famous "blast off". The flock can be as large as 20,000 geese or more.
Species: Snow goose, Chen caerulescens
Location: Bosque del Apache National Wildlife Refuge, Socorro, New Mexico
Image ID: 38738
Species: Snow goose, Chen caerulescens
Location: Bosque del Apache National Wildlife Refuge, Socorro, New Mexico
Image ID: 38738

La Jolla Cove and Point La Jolla at Dawn, waves blur into abstract white, pre-sunrise soft light.
Location: La Jolla, California
Image ID: 38916
Panorama dimensions: 5384 x 10917
Location: La Jolla, California
Image ID: 38916
Panorama dimensions: 5384 x 10917

Snow geese fly in huge numbers at sunrise. Thousands of wintering snow geese take to the sky in predawn light in Bosque del Apache's famous "blast off". The flock can be as large as 20,000 geese or more.
Species: Snow Goose, Chen caerulescens
Location: Bosque del Apache National Wildlife Refuge, Socorro, New Mexico
Image ID: 39904
Panorama dimensions: 5566 x 8349
Species: Snow Goose, Chen caerulescens
Location: Bosque del Apache National Wildlife Refuge, Socorro, New Mexico
Image ID: 39904
Panorama dimensions: 5566 x 8349

Snow geese fly in huge numbers at sunrise. Thousands of wintering snow geese take to the sky in predawn light in Bosque del Apache's famous "blast off". The flock can be as large as 20,000 geese or more.
Species: Snow Goose, Chen caerulescens
Location: Bosque del Apache National Wildlife Refuge, Socorro, New Mexico
Image ID: 39905
Species: Snow Goose, Chen caerulescens
Location: Bosque del Apache National Wildlife Refuge, Socorro, New Mexico
Image ID: 39905

Snow geese fly in huge numbers at sunrise. Thousands of wintering snow geese take to the sky in predawn light in Bosque del Apache's famous "blast off". The flock can be as large as 20,000 geese or more.
Species: Snow Goose, Chen caerulescens
Location: Bosque del Apache National Wildlife Refuge, Socorro, New Mexico
Image ID: 39931
Species: Snow Goose, Chen caerulescens
Location: Bosque del Apache National Wildlife Refuge, Socorro, New Mexico
Image ID: 39931

Gray whales at sunset, Laguna San Ignacio.
Species: Gray whale, Eschrichtius robustus
Location: San Ignacio Lagoon, Baja California, Mexico
Image ID: 03387
Species: Gray whale, Eschrichtius robustus
Location: San Ignacio Lagoon, Baja California, Mexico
Image ID: 03387

Fantastic colorful sedimentary patterns, Bentonite layers are seen as striations exposed in the Utah Badlands. The Bentonite Hills are composed of the Brushy Basin shale member of the Morrison Formation. This layer was formed during Jurassic times when mud, silt, fine sand, and volcanic ash were deposited in swamps and lakes. Aerial photograph.
Location: Utah
Image ID: 38029
Location: Utah
Image ID: 38029

La Jolla Cove and Point La Jolla at Dawn, waves blur into abstract white, pre-sunrise soft light.
Location: La Jolla, California
Image ID: 38915
Location: La Jolla, California
Image ID: 38915

Scripps Pier, predawn abstract study of pier pilings and moving water.
Location: Scripps Institution of Oceanography, La Jolla, California
Image ID: 26340
Location: Scripps Institution of Oceanography, La Jolla, California
Image ID: 26340

Double-crested cormorants in flight at sunrise, long exposure produces a blurred motion.
Species: Double-crested cormorant, Phalacrocorax auritus
Location: La Jolla, California
Image ID: 15280
Species: Double-crested cormorant, Phalacrocorax auritus
Location: La Jolla, California
Image ID: 15280

Beautiful underwater sunburst, glittering light through the ocean surface, Sea of Cortez, Baja California, Mexico.
Location: Sea of Cortez, Baja California, Mexico
Image ID: 27562
Location: Sea of Cortez, Baja California, Mexico
Image ID: 27562

Snow geese at sunrise. Thousands of wintering snow geese take to the sky in predawn light in Bosque del Apache's famous "blast off". The flock can be as large as 20,000 geese or more. Long time exposure creates blurring among the geese.
Species: Snow goose, Chen caerulescens
Location: Bosque del Apache National Wildlife Refuge, Socorro, New Mexico
Image ID: 21799
Species: Snow goose, Chen caerulescens
Location: Bosque del Apache National Wildlife Refuge, Socorro, New Mexico
Image ID: 21799

Snow geese fly in huge numbers at sunrise. Thousands of wintering snow geese take to the sky in predawn light in Bosque del Apache's famous "blast off". The flock can be as large as 20,000 geese or more.
Species: Snow goose, Chen caerulescens
Location: Bosque del Apache National Wildlife Refuge, Socorro, New Mexico
Image ID: 38770
Species: Snow goose, Chen caerulescens
Location: Bosque del Apache National Wildlife Refuge, Socorro, New Mexico
Image ID: 38770

Snow geese fly in huge numbers at sunrise. Thousands of wintering snow geese take to the sky in predawn light in Bosque del Apache's famous "blast off". The flock can be as large as 20,000 geese or more.
Species: Snow Goose, Chen caerulescens
Location: Bosque del Apache National Wildlife Refuge, Socorro, New Mexico
Image ID: 39906
Species: Snow Goose, Chen caerulescens
Location: Bosque del Apache National Wildlife Refuge, Socorro, New Mexico
Image ID: 39906

Snow geese fly in huge numbers at sunrise. Thousands of wintering snow geese take to the sky in predawn light in Bosque del Apache's famous "blast off". The flock can be as large as 20,000 geese or more.
Species: Snow Goose, Chen caerulescens
Location: Bosque del Apache National Wildlife Refuge, Socorro, New Mexico
Image ID: 39930
Species: Snow Goose, Chen caerulescens
Location: Bosque del Apache National Wildlife Refuge, Socorro, New Mexico
Image ID: 39930

Snow geese fly in huge numbers at sunrise. Thousands of wintering snow geese take to the sky in predawn light in Bosque del Apache's famous "blast off". The flock can be as large as 20,000 geese or more.
Species: Snow goose, Chen caerulescens
Location: Bosque del Apache National Wildlife Refuge, Socorro, New Mexico
Image ID: 38756
Species: Snow goose, Chen caerulescens
Location: Bosque del Apache National Wildlife Refuge, Socorro, New Mexico
Image ID: 38756

Snow geese fly in huge numbers at sunrise. Thousands of wintering snow geese take to the sky in predawn light in Bosque del Apache's famous "blast off". The flock can be as large as 20,000 geese or more.
Species: Snow goose, Chen caerulescens
Location: Bosque del Apache National Wildlife Refuge, Socorro, New Mexico
Image ID: 38761
Species: Snow goose, Chen caerulescens
Location: Bosque del Apache National Wildlife Refuge, Socorro, New Mexico
Image ID: 38761

The Mandelbrot Fractal. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set.
Species: Mandelbrot fractal, Mandelbrot set
Image ID: 10368
Species: Mandelbrot fractal, Mandelbrot set
Image ID: 10368

The Mandelbrot Fractal. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set.
Species: Mandelbrot fractal, Mandelbrot set
Image ID: 10369
Species: Mandelbrot fractal, Mandelbrot set
Image ID: 10369


