 |
|
|
| Surf grass on the rocky reef -- appearing blurred in this time exposure -- is tossed back and forth by powerful ocean waves passing by above. San Clemente Island. Image ID: 10237 Species: Surfgrass, Phyllospadix Location: San Clemente Island, California, USA | Clouds light up with blazing colors at sunset. Image ID: 04819 Location: La Jolla, California, USA | Gray whales at sunset, Laguna San Ignacio. Image ID: 03387 Species: Gray whale, Eschrichtius robustus Location: San Ignacio Lagoon, Baja California, Mexico |
|
|
|
| Beautiful underwater sunburst, glittering light through the ocean surface, Sea of Cortez, Baja California, Mexico. Image ID: 27562 Location: Sea of Cortez, Baja California, Mexico | The Mandelbrot Fractal. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set. Image ID: 10368 Species: Mandelbrot fractal, Mandelbrot set | The Mandelbrot Fractal. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set. Image ID: 10369 Species: Mandelbrot fractal, Mandelbrot set |
|
|
|
| Detail within the Mandelbrot set fractal. This detail is found by zooming in on the overall Mandelbrot set image, finding edges and buds with interesting features. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set. 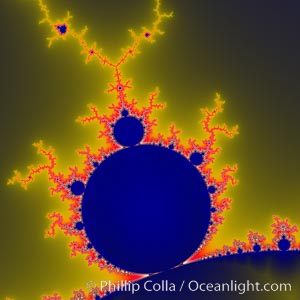Image ID: 10375 Species: Mandelbrot fractal, Mandelbrot set | Detail within the Mandelbrot set fractal. This detail is found by zooming in on the overall Mandelbrot set image, finding edges and buds with interesting features. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set. Image ID: 10378 Species: Mandelbrot fractal, Mandelbrot set | Detail within the Mandelbrot set fractal. This detail is found by zooming in on the overall Mandelbrot set image, finding edges and buds with interesting features. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set. Image ID: 10383 Species: Mandelbrot fractal, Mandelbrot set |
|
|
|
| Detail within the Mandelbrot set fractal. This detail is found by zooming in on the overall Mandelbrot set image, finding edges and buds with interesting features. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set. Image ID: 10391 Species: Mandelbrot fractal, Mandelbrot set | Detail within the Mandelbrot set fractal. This detail is found by zooming in on the overall Mandelbrot set image, finding edges and buds with interesting features. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set. Image ID: 10395 Species: Mandelbrot fractal, Mandelbrot set | The Mandelbrot Fractal. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set. Image ID: 18729 Species: Mandelbrot fractal, Mandelbrot set |
|
|
|
| The Mandelbrot Fractal. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set. Image ID: 18731 Species: Mandelbrot fractal, Mandelbrot set | Fractal design. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set. Image ID: 18732 Species: Mandelbrot fractal, Mandelbrot set | The Mandelbrot Fractal. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set. Image ID: 18737 Species: Mandelbrot fractal, Mandelbrot set |
|
|
|
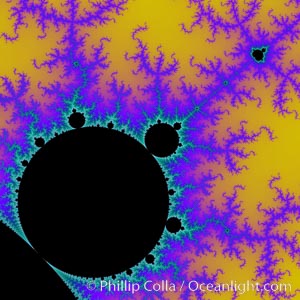
| The Mandelbrot Fractal. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set. Image ID: 18739 Species: Mandelbrot fractal, Mandelbrot set | Clouds held back by island crest. Image ID: 03848 Location: Guadalupe Island (Isla Guadalupe), Baja California, Mexico | A garibaldi fish (orange), surf grass (green) and palm kelp (brown) on the rocky reef -- all appearing blurred in this time exposure -- are tossed back and forth by powerful ocean waves passing by above. San Clemente Island. Image ID: 10238 Species: Surfgrass, Hypsypops rubicundus, Phyllospadix Location: San Clemente Island, California, USA |
|
|
|
| Beautiful underwater sunburst, glittering light through the ocean surface, Sea of Cortez, Baja California, Mexico. Image ID: 27561 Location: Sea of Cortez, Baja California, Mexico | North Pacific humpback whale, blow at sunset. Image ID: 05883 Species: Humpback whale, Megaptera novaeangliae Location: Maui, Hawaii, USA | Sunrise light on clouds. Image ID: 06225 |
|
|
|
| Beautiful underwater sunburst, glittering light through the ocean surface, Sea of Cortez, Baja California, Mexico. Image ID: 27569 Location: Sea of Cortez, Baja California, Mexico | Beautiful underwater sunburst, glittering light through the ocean surface, Sea of Cortez, Baja California, Mexico. Image ID: 27570 Location: Sea of Cortez, Baja California, Mexico | Land visit and sunset, skiff and tourists. Image ID: 03474 Location: Floreana Island, Galapagos Islands, Ecuador |
|
|
|
| Point Loma lighthouse. Image ID: 05510 Location: San Diego, California, USA | Cabrillo Monument lighthouse at sunset, Point Loma. Image ID: 05511 Location: San Diego, California, USA | Sunset reflections in the Tuolumne River. Image ID: 09975 Location: Tuolumne Meadows, Yosemite National Park, California, USA |
|
|
|
| Surf grass on the rocky reef -- appearing blurred in this time exposure -- is tossed back and forth by powerful ocean waves passing by above. San Clemente Island. Image ID: 10247 Species: Surfgrass, Phyllospadix Location: San Clemente Island, California, USA | Clouds form at dawn before a storm rolls in. Image ID: 22474 Location: Carlsbad, California, USA | Clouds form at dawn before a storm rolls in. Image ID: 22475 Location: Carlsbad, California, USA |
Natural History Photography Blog posts (6) related to Abstracts And Patterns
Alternative Search:
Related Topics:
Keywords: