Fractals

By February 2, 2005Photo of the Day

Recently we were approached about producing Fractal Images for a client. With the correct software, and a sufficiently powerful computer, these are quite simple to create. Here are a few examples we made:

The Mandelbrot Fractal. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set, Mandelbrot set

The Mandelbrot Fractal. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set.
Image ID: 10370
Species: Mandelbrot Fractal, Mandelbrot set

Detail within the Mandelbrot set fractal. This detail is found by zooming in on the overall Mandelbrot set image, finding edges and buds with interesting features. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set, Mandelbrot set

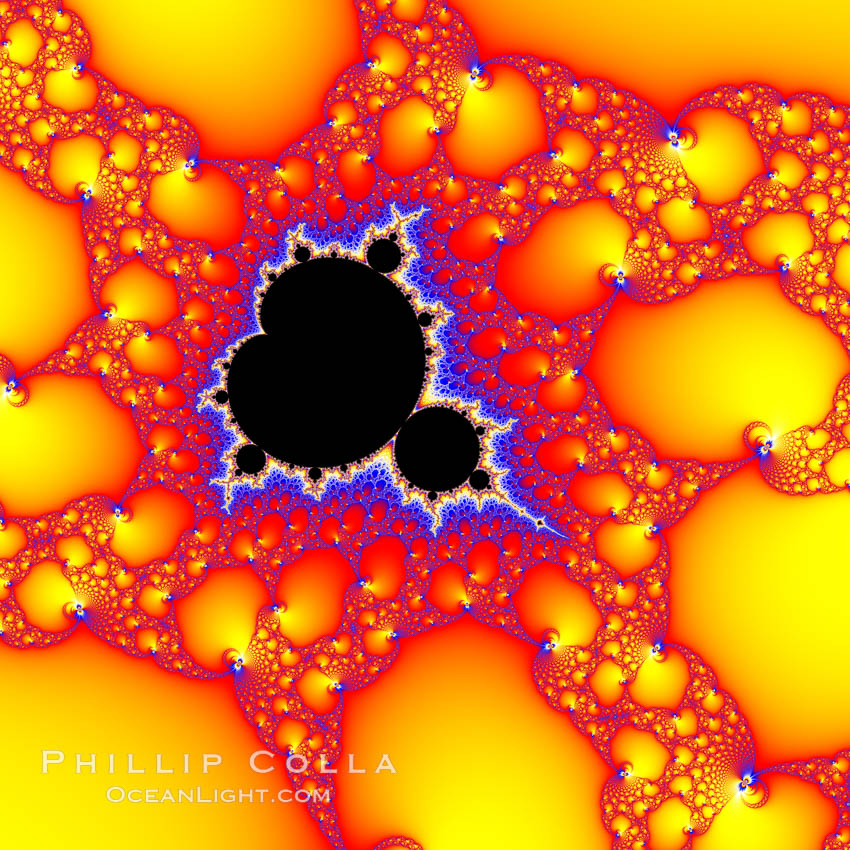
Detail within the Mandelbrot set fractal. This detail is found by zooming in on the overall Mandelbrot set image, finding edges and buds with interesting features. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set.
Image ID: 10376
Species: Mandelbrot Fractal, Mandelbrot set

Detail within the Mandelbrot set fractal. This detail is found by zooming in on the overall Mandelbrot set image, finding edges and buds with interesting features. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set, Mandelbrot set

Detail within the Mandelbrot set fractal. This detail is found by zooming in on the overall Mandelbrot set image, finding edges and buds with interesting features. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set.
Image ID: 10383
Species: Mandelbrot Fractal, Mandelbrot set

Detail within the Mandelbrot set fractal. This detail is found by zooming in on the overall Mandelbrot set image, finding edges and buds with interesting features. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set, Mandelbrot set

Detail within the Mandelbrot set fractal. This detail is found by zooming in on the overall Mandelbrot set image, finding edges and buds with interesting features. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set.
Image ID: 10391
Species: Mandelbrot Fractal, Mandelbrot set

A fractal is a geometric object which can be divided into parts, each of which is similar to the original object. Fractals are said to possess infinite detail, and are generally self-similar and independent of scale. In many cases a fractal can be generated by a repeating pattern, typically a recursive or iterative process. The term fractal was coined in 1975 by Benoît Mandelbrot, from the Latin fractus or “broken”.

The Mandelbrot set, named after its discoverer, is a famous example of a fractal.Fractals of many kinds were originally studied as mathematical objects. Fractal geometry is the branch of mathematics which studies the properties and behaviour of fractals. It describes many situations which cannot be explained easily by classical geometry, and has often been applied in science, technology, and computer-generated art. The conceptual roots of the fractals can be traced to attempts to measure the size of objects for which traditional definitions based on Euclidean geometry or calculus fail.

Here are all of the fractals we have produced so far.

Here are more fractal pictures.

Keywords: fractals, fractal, fractal picture, fractal pictures, Mandelbrot set, fractal geometry, photograph

About Phil Colla

I am a natural history photographer. I enjoy making compelling images in the ocean, on land, and in the air. I have maintained the Natural History Photography blog since 2005 and my searchable Natural History Photography Library since 1997. Here are some tear sheets and behind the scenes views. Thanks for looking!

Next Post